3x+1转换
3x+1：任意给定一个自然数n，当n是偶数时，将它除以2，即将它变成n/2；当n是奇数时，就将它变成3n+1，经过若干步后，总会得到1。
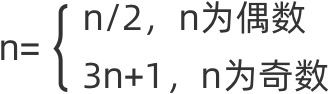
对于任意一个自然数n,我们把除以2记为0，乘以3加1标记为1，则自然数可以用01序列来表示。因为一个奇数通过乘以3加1后一定是偶数，故01序列不可能出现两个1相临。反过来，满足条件的01序列也能表示一个整数。
3X+1树图
G序列与x+1序列的树图结构完全相同，我们统计他们表示数的一些对应规律，探索两者对应的一些特征。
(3x+1)/2树图
(3x+1)/2：对于3x+1,因为n为奇数时，经过3x+1必定为偶数，可以将3n+1和除以2合并成,即
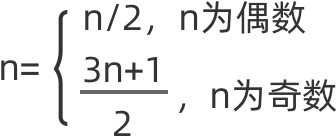
类似3x+1,我们同样可以作出相对应的树图。
x+1转换
角谷3x+1的性质非常复杂，他的统计性质和规律都比较复杂，我们考虑一个简化版本x+1,可以通过研究x+1的一些规律去探寻3x+1的一些性质。
x+1：任意给定一个自然数n，当n是偶数时，将它除以2，即将它变成n/2；当n是奇数时，就将它变成n+1，经过若干步后，总会得到1。
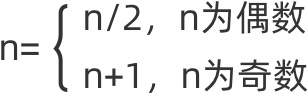
类似3x+1,我们可以将一个整数用x+1的01序列来表示，可以看到x+1的01序列唯一的要求是两个1不能相邻，有非常好的性质，01序列和整数的转换能够用解释的形式来表示，每一层的个数符合斐波那契数列。
x+1性质
对于一个x+1的01序列，他表示的整数的大小范围完全由0的个数决定，比如0的个数为n,则它表示的整数范围为2^n ~2^(n+1),因此我们可以以2^n为起点去查找我们需要表达的目标数。
x+1树图
类似3x+1，我们可以作出角谷x+1的树形图，连接左子节点的边表示0，连接右子节点的边表示1，对应于x+1操作中的乘以2和加上1，一条边不能够连接两个1。所有的整数都对应树图上的唯一一个节点，树图每一层的个数为斐波那契数列。
